The term “Millennial problems” encapsulates the unique challenges and opportunities faced by the generation that came of age at the turn of the 21st century. Born between the early 1980s and the mid-1990s, millennials have witnessed the rapid evolution of technology, shifts in the job market, and changes in societal norms. In this article, we will discuss the distinctive issues that define the millennial experience, exploring how this generation is forging its path in an ever-changing world.
The term “Millennium Problems” refers to a set of seven unsolved mathematical problems, including P vs. NP, that were designated by the Clay Mathematics Institute in the year 2000. The institute offered a prize of one million dollars for the solution to each of these problems. These problems are:
Birch and Swinnerton- Dyer Conjecture
It deals with elliptic curves and their connection to the distribution of rational points on the curve.
Hodge Conjecture
This problem is related to algebraic cycles and their cohomology classes in complex algebraic varieties.
Navier–Stokes Existence and Smoothness
It concerns the behaviour of incompressible fluid flow and the question of whether smooth solutions always exist for certain conditions.
P versus NP Problem
One of the most famous problems in computer science, it asks whether every problem with a verifiable solution can also be solved quickly (in polynomial time).
Poincaré Conjecture
This problem was famously solved by Grigori Perelman in 2003 and deals with the topology of 3-dimensional spaces.
Riemann Hypothesis
This is a fundamental conjecture about the distribution of nontrivial zeros of the Riemann zeta function, a complex analytic function.
Yang-Mills Existence and Mass Gap
This problem is related to quantum field theory and the behaviour of particles in the universe, specifically whether certain quantum fields have a mass gap.
Puzzling Over P vs. NP
In the intricate world of computer science and mathematics, there exists a conundrum that has stymied the greatest minds for decades – the P vs. NP problem. This problem is like the Rubik’s Cube of the digital age, a riddle that, once solved, could unlock a treasure trove of possibilities for the tech-savvy world we live in.
P vs NP Demystified
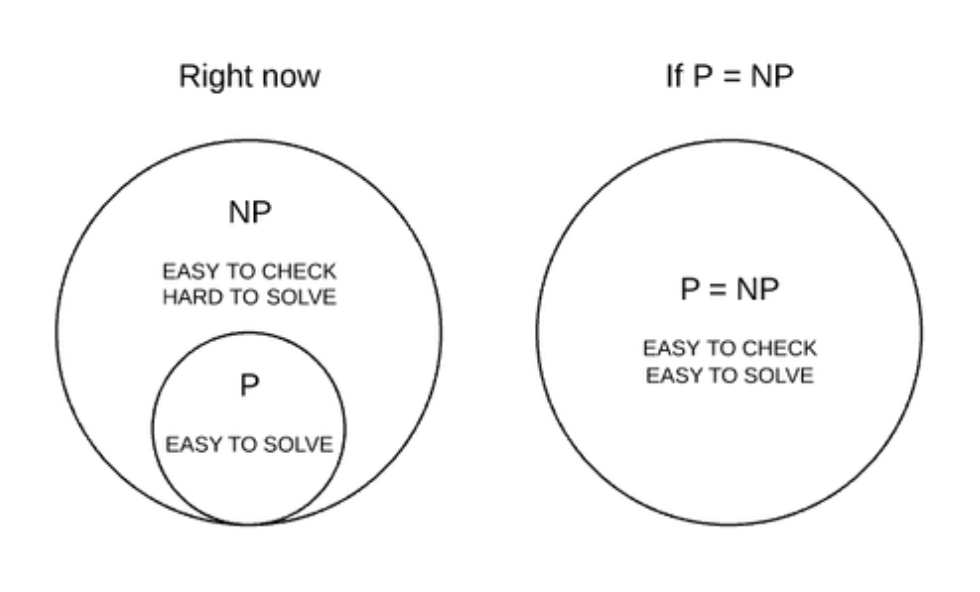
P: Problems with Efficiency
Imagine cooking your favourite meal with a well-detailed recipe in hand. You can efficiently follow the steps and produce a delicious dish. Such problems, where you can verify the solution quickly, are termed P problems. In essence, P problems are tasks that can be efficiently tackled by computers.
NP: Non-Polynomial Puzzles
Now, consider the challenge of solving a jigsaw puzzle without seeing the final image. It’s easier to check if someone else has solved it correctly than to complete it yourself. These are the NP problems, where verifying a solution is much simpler than finding it. NP problems encompass a vast array of challenges, from optimizing routes to decoding genetic sequences.
The Significance of P vs NP: A Computing Revolution
Understanding P vs. NP is not just a mathematical curiosity; it has profound real-world implications. Let’s first consider the scenario where P equals NP:
Faster Computing
If P equals NP, in millennium Problems, it means we have efficient algorithms for solving many complex problems. Think of route optimization for delivery trucks, where the best path can be found quickly, leading to cost savings and faster deliveries.
Medical Research
In the realm of medical research, finding cures for diseases, creating vaccines, and understanding the human genome could become dramatically more efficient. Researchers could process vast amounts of data and simulate complex biological systems with ease.
Data Analysis
Businesses could harness the power of data like never before. Complex data analysis, market predictions, and recommendation systems could provide more accurate and rapid insights.
But What if P Doesn’t Equal NP?
The other possibility is that P doesn’t equal NP, which suggests that some problems are inherently hard to solve efficiently. This has far-reaching consequences:
Computer Security
The foundation of online security relies on the assumed difficulty of certain mathematical problems. If P doesn’t equal NP, encryption methods remain secure, safeguarding sensitive data during online transactions.
Cryptography: Cryptographic systems that protect personal information, financial data, and communication channels will remain robust. The security of online banking, email, and data privacy will remain intact.
The Dark Side of NP
Inefficiency and Consequences
But what if P doesn’t equal NP in millennium Problems? That means some problems might be inherently hard to solve efficiently. Consider online banking and data privacy – crucial aspects of our digital world. If NP problems remain intractable, it could spell trouble for computer security and cryptography. Your online transactions and sensitive data may not be as secure as we hope.
The Challenge of P vs. NP

A Daunting Puzzle
Why is the P vs. NP problem so elusive? To answer this, we must delve into the complexity of the problem itself. The search space for potential solutions is vast, making it akin to finding a needle in a cosmic haystack. Despite the combined efforts of brilliant mathematicians and computer scientists, the solution remains elusive.
The Future of P vs. NP
As we conclude our journey through the enigmatic world of P vs. NP, a millennium Problem, we leave you with one thought: What if? What if this age-old puzzle is finally solved? The impact on our digital world would be monumental, shaping the course of technology and science in ways we can only begin to imagine.
Conclusion
The P vs. NP problem continues to perplex and inspire. It is a testament to human curiosity and the unyielding pursuit of knowledge. As technology advances, so does our understanding of this enigma. Whether it’s the keys to a brighter digital future or the acceptance of its inherent challenges, P vs NP remains an enduring quest for answers.
FAQs (Frequently Asked Questions)
1. What does P vs NP stand for?
P vs NP refers to a fundamental problem in computer science and mathematics that deals with the efficiency of solving computational problems.
2. How can solving the P vs NP problem benefit us?
Solving P vs NP could revolutionize computing, leading to faster solutions for complex problems in various fields like medicine, logistics, and data analysis.
3. Are there any downsides to P vs NP being unsolved?
Yes, if P doesn’t equal NP, it means some problems are inherently hard to solve efficiently, which could have consequences for computer security and cryptography.
4. Why is the P vs NP problem so challenging to solve?
The P vs NP problem is challenging due to the immense complexity of the problem and the vast search space for potential solutions.
5. What is the significance of P vs NP in everyday life?
P vs NP has the potential to impact various aspects of our daily lives, from improving the efficiency of everyday tasks to advancing scientific research and technology.








